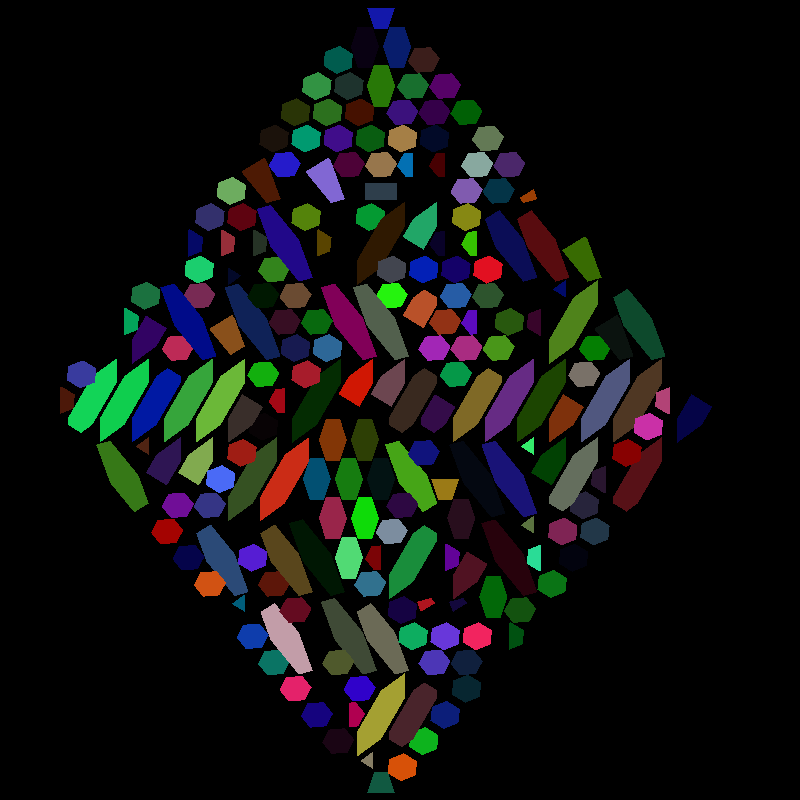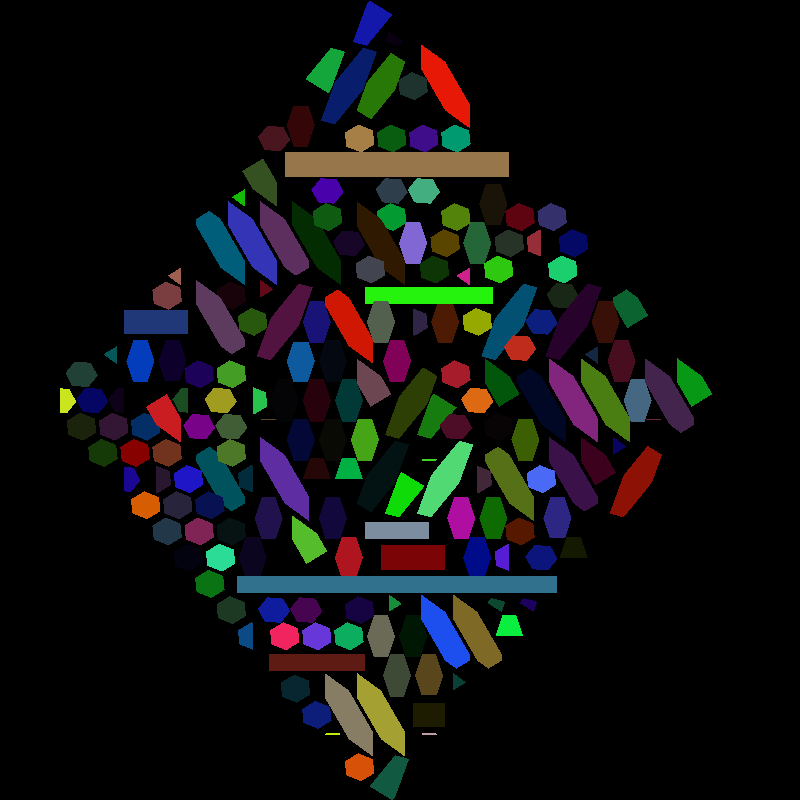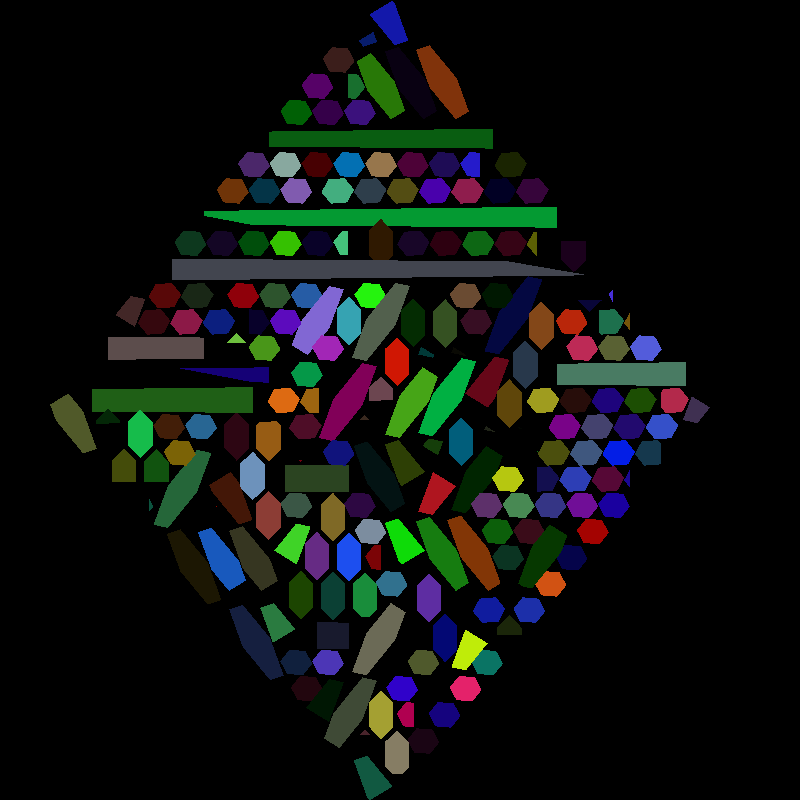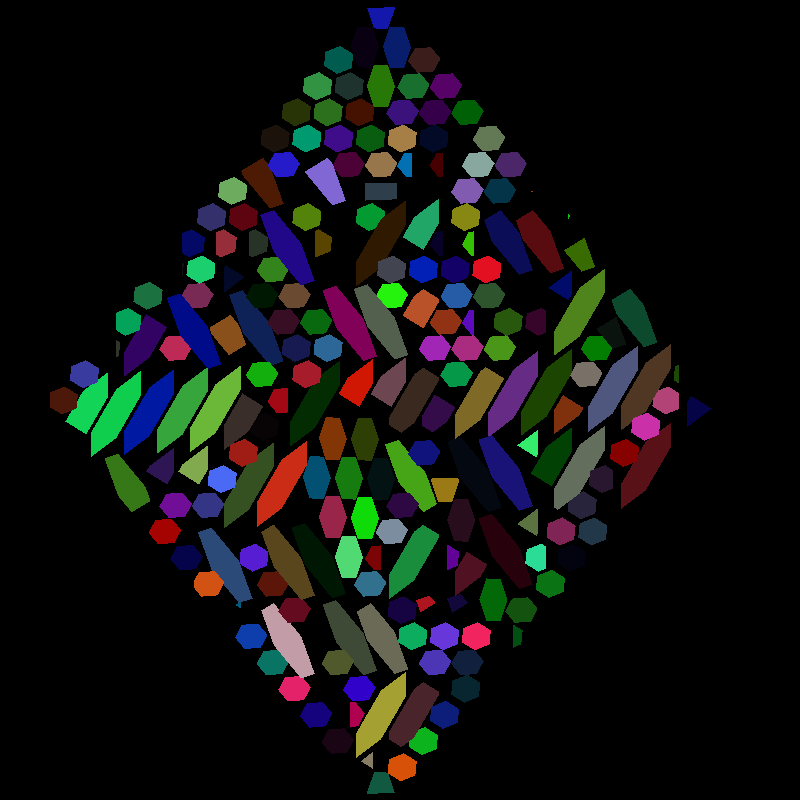When visiting the Smithsonian Natural History Museum, I saw the inside of a meteorite, stained and polished to reveal a beautiful pattern. Several months later, I remembered it while looking through some photos and decided to learn more about it and try to reproduce it.
Here’s what I learned from Wikipedia: The meteorites that display this pattern are comprised of of two Iron-Nickel alloys, Kamacite and Taenite. This pattern is found in metiorites called Octahidrites, so named because the pattern is actually a result of a crystal structure of Taenite’s crystal latice, which is hexoctahedral (cubic) in structure. The pattern generated when such a crystal is sliced along a “face” of the crystal is the Widmanstätten pattern, but cut along different axes you will see different patterns (a square equivalent to the Widmanstatten, or just chaotic beauty if not at a multiple of 15 degrees). Wikipedia’s image here speaks a thousand words:
 (Source Davide Bolsi - Different cuts of the octaedron produces different kinds of Widmanstätten patterns. CC BY-SA 3.0, unedited, Created 9 June 2008, https://en.wikipedia.org/wiki/Widmanst%C3%A4tten_pattern#Shape_and_orientation)
(Source Davide Bolsi - Different cuts of the octaedron produces different kinds of Widmanstätten patterns. CC BY-SA 3.0, unedited, Created 9 June 2008, https://en.wikipedia.org/wiki/Widmanst%C3%A4tten_pattern#Shape_and_orientation)
So I tried to simulate this, with some mixed effects!
It took me a long time to figure out how to render it (ended up using polygon intersections using Java’s euclidean threed library with raw writing to pngs with the results). Also took me a long time to debug all 35 major bugs in my code (I kept track after I started getting rendered output to show the progression, maybe a topic for another post!). The end results are below:
An face cut, producing the iconic Widmanstätten pattern. 

A square cut, producing the less iconic (but verifying) crosshatch pattern. 

But I didn’t think these captured the 3D crystal aspect of the project, so I also animated a plane passing through the crystal perpendicular to the face cut: 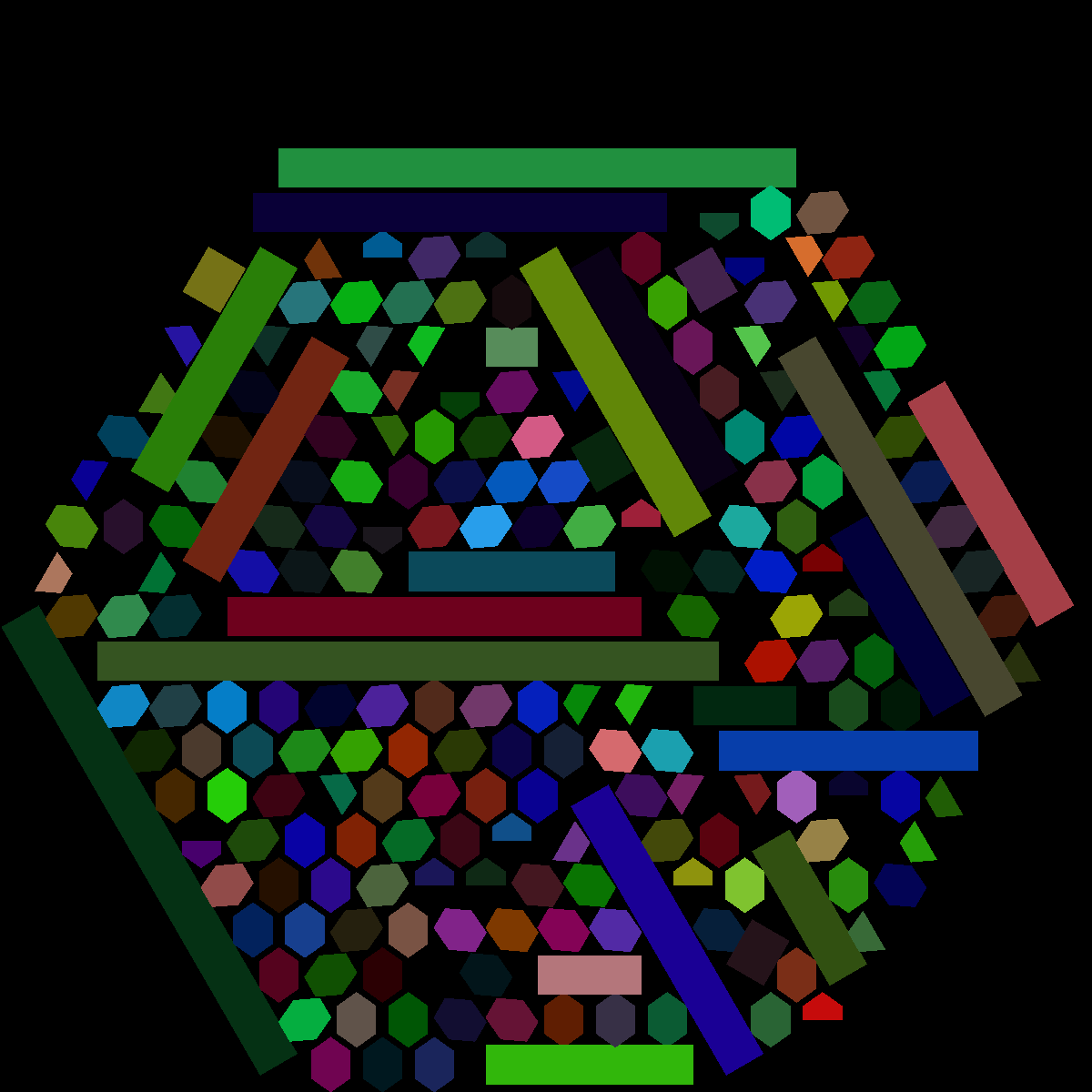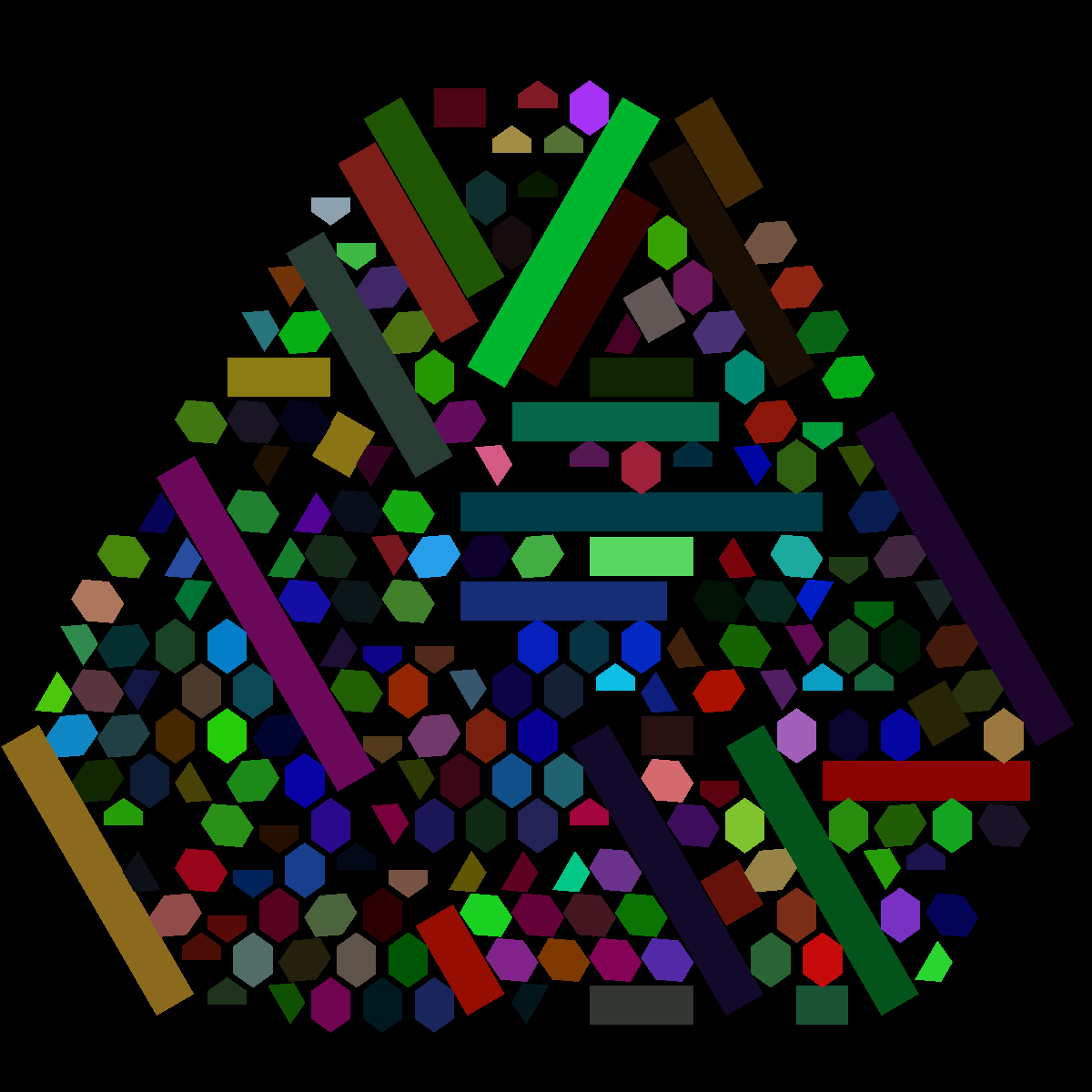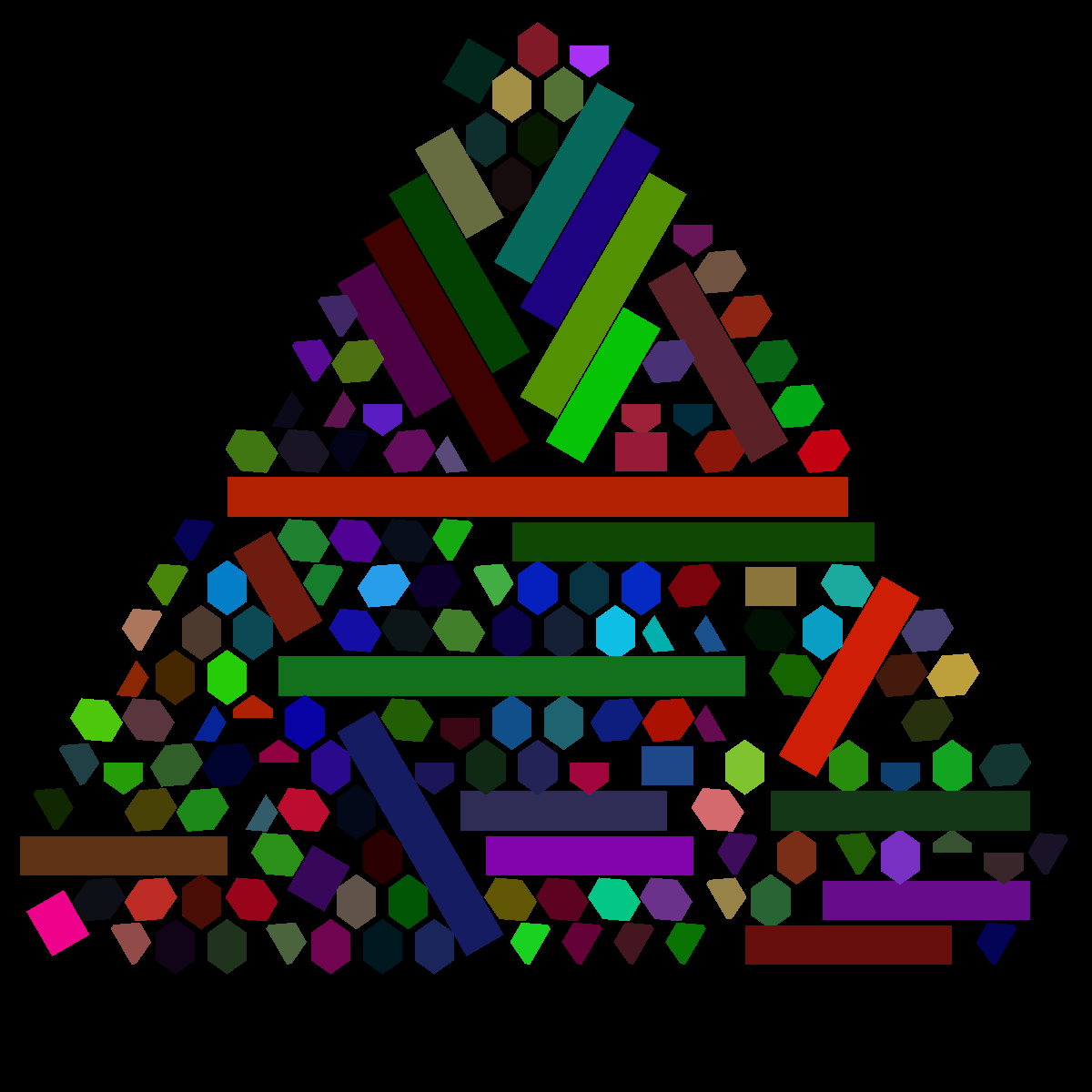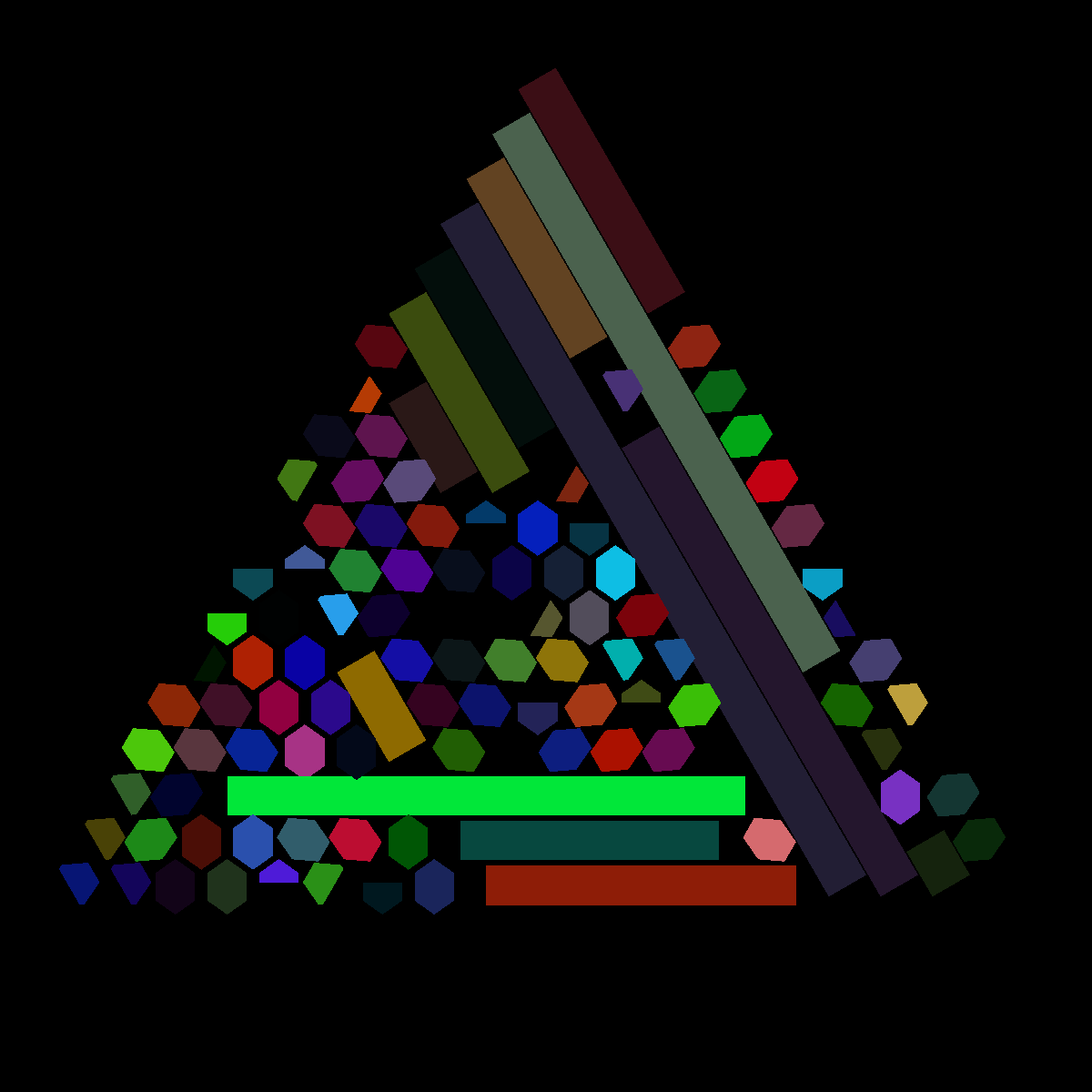

And animated rotations (aligned with the square and face cuts) that rotate through all the other angles perpendicular ot the face or square cuts. This helps you see the patterns align with the cut angle and then unalign at values that aren’t multiples of 15.